|
P
|
ARENTESC I CONSANGUINITAT (2) |
|
www.labordadurtx.org
>> articles >>parentiu (2)
|
En l'article anterior definíem alguns dels conceptes bàsics per a poder entendre millor el significat de parentesc i consanguinitat. Malgrat i tenint en compte que l'estudi de la transmissió de gens es basa en el càlcul de probabilitats, no queda sobrat repassar algunes definicions.
cada vegada que tirem una moneda a l'aire, tan pot sortir cara com creu, i com que això succeeix sempre, decidim que és igualment probable que surti cara o creu, o sigui que la probabilitat és la mateixa. Com que de dos casos possibles, només s'he n'ha de verificar un a cada tirada, diem quela probabilitat que surti cara o creu és 1/2.
Un altre exemple: si suposem el cas del dau, en tirar-lo tenim sis possibilitats, totes elles equiparables, pot sortir 1, 2, 3, 4, 5 o 6. Per tant, seguint el mateix raonament anterior, la porobabilitat de cada vegada serà 1/6.
En general, la probabilitat d'un succés que es presenta en "c" casos favorables sobre "C", casos possibles, el trobarem pel coeficient de:
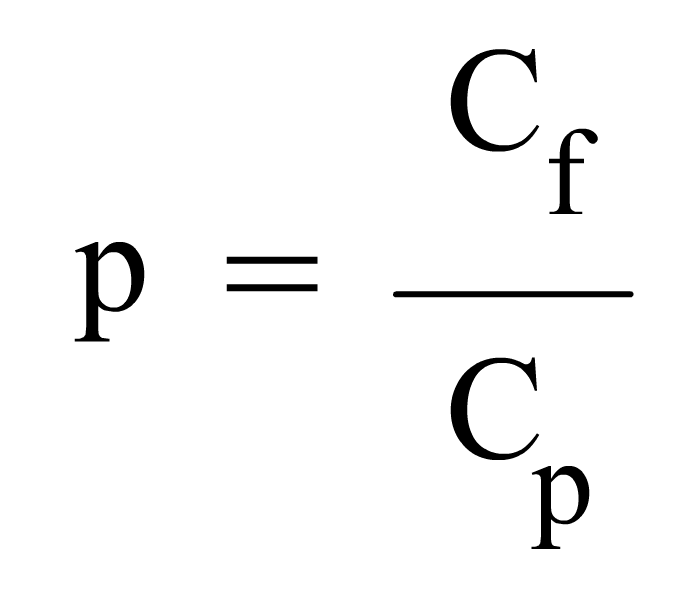 |
si un succés es presenta sempre, la seva probabilitat és de u i diem d'ell que és segur; si no es presenta mai, la seva probabilitat és zero i diem d'ell que és impossible
En el cas de la transmissió genètica, cada individu trespassa, sempre, la meitat dels seus gens o sigui, un de cada dos cromosomes homòlegs, i com que això es produeix a l'atzar, la probabilitat de que traspassi uns o altres serà 1/2.
Per exemple, en la transmissió de gens la probabilitat que un individu rebi uns gens determinats d'un abantpassat seu, ve donada pel producte de les probabilitats de transmissió d'aquests gens en cada generació, des de l'abantpassat fins aquest individu. Veiem que el pas dels gens d'una generació a una altra és un fet independent en cada generació però el conjunt de gens de l'individu resultant depèn de com s'han transmès els gens des de l'abantpassat fins arribar a ell.
Com que la probabilitat de transmissió dels gens en cada generació sempre és 1/2, només haurem de multiplicar aquesta xifra per si mateixa tantes vegades com generacions separen a aquest individu del seu abantpassat.
Una vegada fet aquest petit repàs de càlcul de probabilitats
ja podem desenvolupar els conceptes de consanguinitat i parentesc.
La consanguinitat es pot definir com el creuament entre individus emparentats. Com més gran sigui el parentesc entre els dos individus, més gran serà el coeficient de consanguinitat dels seus descendents i menor serà la probabilitat de què el conjunt dels cadells sigui heterozigòtica.
Començarem considerant la situació més senzilla possible: dos descendents B i C que tenen un progenitor A en comú. Utilitzant fletxes per indicar la direcció de l'herència, aquesta situació es pot representar de la següent manera:
|
|
|
figura 1
|
On A és l'abantpassat comú de B i C. Si B i C reben una còpia del mateix gen, és a dir, el mateix segment d'ADN d'un locus qualsevol d'A, podem dir que B i C tenen gens que són idèntics per descendència procedents d'A. Recordem que dos gens són idèntics per descendència si són còpies del mateix segment d'ADN.
Suposem que B i C es creuen per produir un descendent O:
|
|
|
figura 2
|
Si B i C tenen gens que són idèntics per descendència, en qualsevol locus existeix una certa probabilitat que O heredi dos gens que són idèntics per descendència, un precedent d'A a través de B i un altre procedent d'A a través de C. Estem en disposició de definir el coeficient de consanguinitat:
"El coeficient de consanguinitat d'un individu és la probabilitat que dos gens presents en un locus de l'individu siguin identics per descendència."
El coeficient de consanguinitat es designa generalment mitjançant la lletra F. Si un individu té dos gens que són idèntics per descendència en un determinat locus, serà homozigot per aquest locus. Per tant, el coeficient de consanguinitat és un reflexe de la homozigosis.
En genètica es defineix com a població a un grup d'individus que s'entrecreuen i comparteixen un patrimoni comú de gens que es transmeten de generació en generació d'acord amb les lleis de Mendel. Per a mesurar el coeficient de consanguinitat es pren com a base a un grup d'individus, (d'aquí el nom de població base), que se suposa que no estan emparentats.
És important tenir en compte que el coeficient de consanguinitat no medeix la homozigosis en sentit absolut. De fet, és una quantitat relativa que medeix el descens de la heterozigosis en relació a una població base on tots els individus, se suposa, no estan relacionats i tenen una consanguinitat zero. En definitiva, medeix el grau en què un individu és menys heterozigocit que els individus que suposadament tenen consanguinitat zero. A la pràctica, suposem que tenen consanguinitat zero (F=0), tots aquells individus dels que no disposem d'informació.
Per calcular el descens de le heterozigosis es resta de la unitat (heterocigosis total) el coeficient de consanguinitat F: (1-F).
Però no podem oblidar que pel sol fet que el Montanya és raça pura, els individus que conformen la població base de la què partim en cada cas, ja porten implícit un elevat nivell d'homozigosis en molts dels seus loci, producte d'una consanguinitat ancestral. Els homozigosits en aquesta població base tenen gens que són considerats com a "similars en estat" i no idèntics per descendència. Això significa que són idèntics en l'estructura perquè tenen la mateixa seqüència d'ADN, i encara així, no són idèntics per descendència perquè provenen de diferents progenitors. Dit d'una altra manera, són homozigòcits per còpies de diferents gens que provenen de progenitors ancestrals, i no per dues còpies d'un únic gen originari d'un progenitor ancestral.
Aleshores és lícit preguntar-nos com les mesures de parentesc i consanguinitat poden ser d'alguna utilitat quan la seva magnitut real depèn de l'elecció arbitrària d'una població base, els membres de la qual se suposa, per conveniència, que no tenen abantpassats comuns.
A primera vista és difícil reconciliar això amb el fet que si retrocedim un número de generacions suficient, dos individus qualsevols han de tenir abantpassats comuns i, per tant, ser parents. A la pràctica això no representa un problema sempre que recordem que els coeficients de parentesc i consanguinitat són quantitats relatives i no absolutes. Així, si un individu té un coeficient de consanguinitat zero relatiu a una determinada població base, la probabilitat que aquest individu sigui heterozigòcit en un locus qualsevol és igual a la freqüència d'heterozigòcits en aquest locus a la població base. Si el nivell d'heterozigosis a la població base és bastant baix, degut, per exemple, a un número significatiu de creuaments entre parents pròxims entre abantpassats de la població base, l'individu amb un coeficient de consanguinitat zero tindrà un nivell bastant baix d'heterozigosis. El punt important és, malgrat tot, que si un segon individu té un coeficient de consanguinitat de 0'3 en relació a la mateixa població base, immediatament sabem que aquest segon individu és un 30% menys heterozigòcit que el individu el coeficient de consanguinitat del qual era zero.
Per un altre cantó, si un individu té un coeficient de consanguinitat de F=1, la probabilitat de que aquest individu sigui heterozigòcit en un locus qualsevol, és igual a zero (1-1=0); ja que l'individu té gens idèntics per descendència en tots els loci, ha de ser necessàriament homocigòcit en tots ells.
Això remarca el fet que els coeficients de consanguinitat permeten comparar els nivells relatius d'heterozigòcits entre individus els pedeegris dels quals poden seguir-se endarrera fins la mateixa població base. Posteriorment analitzarem la fórmula per a calcular el coeficient de consanguinitat.
El parentesc més senzill és aquell existent entre un progenitor (P) i el seu descendent (N). En un locus qualsevol un descendent té dos gens, un dels quals (el gen patern) és una còpia d'un dels gens del pare; i l'altre (el gen matern) és una còpia d'un dels gens de la mare. Donat que això és cert per a tots els loci, podem dir que un descendent comparteix exactament la meitat dels seus gens amb cada un dels seus pares. Amb altres paraules, un progenitor i un descendent tenen exactament la meitat dels seus gens en comú.
Per tant podem definir que: "La proporció esperada de gens en comú entre dos individus no consanguinis és el parentesc entre ells". (Si els individus són consanguinis hem d'aplicar la definició que veurem més endavant amb el parentesc colateral). Per tant el parentesc entre un progenitor i el seu descendent és 1/2 (probabilitat simple). Tan el parentesc directa com el parentesc colateral, que ja el veurem, es designan amb la lletra "a".
Ara, fem-nos la pregunta següent: "Quin és el parentesc entre un descendent (O) i el seu avi (A)?" Per contestar hem de segui la transmissió de gens des de l'avi (A) al pare (P), que a la vegada transmet exactament la meitat dels seus gens a (O). D'aquí que, com a promig, (O) rebrà 1/2 x 1/2 = 1/4 dels seus gens d'(A) (probabilitat composta). Per tant el parentesc entre un descendent i un dels seus avis és 1/4.
No obstant, és important advertir que mentre la proporció real de gens en comú entre un descendent i el seu progenitor és sempre exactament 1/2, la proporció real de gens en comú entre un descendent i el seu avi, i entre tots els parents restants, pot no ser exactament igual a la proporció esperada.
Per exemple, la proporció real de gens en comú entre un determinat descendent i un dels seus quatre avis podria ser major o menor que 1/4. Aquesta proporció podria ser 0 (si es donés el cas que el gàmeta procedent de (P) no hagués portat cap dels gens que (P) va heredar d'(A); o podria valer 1/2 si es donés el cas que el gàmeta procedent de (P) hagués portat tots els gens que (P) va heredar d'(A)).
No hi ha forma de saber la proporció real de gens en comú entre un determinat descendent i un dels seus quatre avis. Com a molt podrem dir que la proporció esperada, és a dir el parentesc, és 1/4.
Mitjançant un raonament semblant al què acabem d'usar, es pot deduir que el prentesc entre un descendent i un dels seus besavis és:
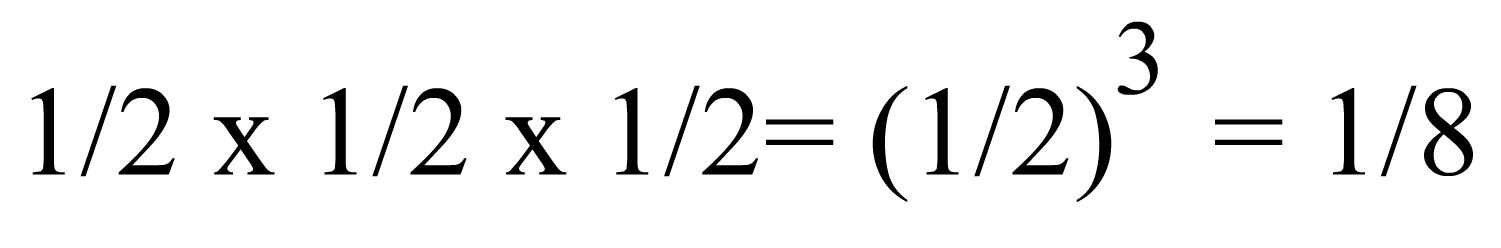 |
En general, el parentesc entre un individu i un dels seus abantpassats disminueix 1/2 per a cada generació que el separa de l'abantpassat.
Per tant, el parentesc entre un individu i un abantpassat qualsevol és:
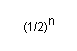 |
on "n" és el número de generacions entre l'individu i el seu abantpassat en la línia de descendència directa de l'abantpassat a l'individu.
Es dedueix que, independentment de la grandesa (entesa com a bon exeplar de raça), que hagi pogut ser un determinat abantpassat, si només apareix una i vàries generacions endarrere en l'arbre genealògic d'un individu, existeix només una petita probabilitat que l'individu en qüestió (al que anomenem O) hagi heredat algun dels gens del seu abantpassat. D'aquí que sigui inútil seleccionar el pedegree d'un individu només perquè un abantpassa contingui pedegree.
La situació és lleugerament diferent si un determinat abantpassat apareix més d'una vegada en l'arbre genaològic. En aquest cas, cada aparició de l'abantpassat en el pedegree proporciona una oportunitat independent que l'individu (O) hagi heredat els gens de l'abantpassat. El parentesc total és, en aquest cas, igual a la suma de les contribucions independents fetes per cada línia de descendència directa.
Per exemple:
|
|
|
figura 3
|
Observem que l'individu B és pare i a la vegada avi d'O. Quin serà el parentesc total entre ells?. En aquest cas hi ha dos línies de descendència directes, per tant, tal com hem anunciat, les seves contribucions al parentesc seran la suma d'ambdues:
 |
El tipo de parentesc que hem conciderat es denomina "parentesc directe" ja que es refereix al parentesc que pot seguir-se en una línia directa o línia de descendència d'abantpassat a descendència. L'altre tipo de parentesc és el mateix que existeix entre dos individus que tenen un abantpassat en comú i poden, per tant, haver heredat el mateix gen d'aquest abantpasat. Aquest tipo de parentesc s'anomena "parentesc colateral".
Conciderem dos descendents, (B) i (C), amb un progenitor (A) en comú, (figura1). En aquest cas, (B) i (C) es diu que són "mig germans" i (A) és el seu abantpassat comú. Si (B) i (C) reben, ambdos, una còpia del mateix gen d'un locus qualsevol d'(A), podem dir que (B) i (C) tenen gens que són idèntics per descendència procedents d'(A).
Ara podem considerar una definició més general del parentesc: "El parentesc entre dos individus qualsevols és el número esperat de gens en un locus d'un individu que són idèntics per descendència amb un gen escollit a l'atzar en el mateix locus de l'altre individu"
Aquesta definició és més correcta que la que hem usat en el parentesc directe, tant si els individus emparentats són consanguinis com si no ho són. Si els individus emparentats no són consanguinis, aquesta definició és equivalent a la que vem oferir pel parentesc directe. Per entendre millor la diferència entre les dues definicions observem la taula següent:
|
Tipo de Gen
|
Coeficient de Consanguinitat
|
Parentesc aditiu entre B i C
|
|||
|
B
|
C
|
FB
|
FC
|
||
|
Definició exacta
|
Definició simple
|
||||
|
A1A2
|
A3A4
|
0
|
0
|
0
|
0
|
|
A1A2
|
A3A2
|
0
|
0
|
1/2
|
1/2
|
|
A1A2
|
A1A2
|
0
|
0
|
1
|
1
|
|
A1A1
|
A1A1
|
1
|
1
|
1
|
2
|
|
taula 1
|
|||||
Com podem veure, la limitació de la definició simple és que no pot distingir entre les dues últimes situacions d'aquesta taula, això vol dir, no pot distingir entre individus que tenen amdos el mateix parell de gens en comú, i dos individus homozigòtics pel mateix gen. Ambdos casos, els dos individus tenen el 100% dels seus gens en comú. Malgrat això, si B i C es creuen, els dos casos diferents donaran lloc a resultats molt diferents respecte al coeficient de consanguinitat de la descendència resultant. En l'últim cas els descendents de B i C tindran, sense dubte, dues còpies del mateix gen A1 i el seu coeficient de consanguinitat serà per tant F = 1 per aquest locus. En canvi, en el cas en que tant B com C siguin A1A2, segons els principis de l'herència mendeliana podem esperar el resultat reflexat a la taula següent:
|
A1
|
A2
|
|
|
A1
|
A1A1
|
A1A2
|
|
A2
|
A2A1
|
A2A2
|
|
taula 2
|
Veiem que la probabilitat que un descendent tingui dues còpies del mateix ges és 1/4 per A1A1 i 1/4 per A2A2, això ens dóna un coeficient de consanguinitat F = 1/4 + 1/4 = 1/2.
Com en el cas dels parents directes, el parentesc entre dos parents colaterals disminueix 1/2 per a cada generació que separa els dos parents al llarg d'un determinat trajecte. La única diferència és que en el cas dels parents colaterals, el trajecte entre ells consta de dues línies de descendència: una des de l'abantpassat comú fins a l'altre parent. Per remarcar això, el número total de generacions que separa als dos parents colaterals s'escriu n + n' , on n és el número de generacions entre l'abantpassat comú i el primer parent, i n' és el número de generacions entre l'abantpassat comú i el segon parent. Així per un trajecte qualsevol, el parentesc entre dos parents colaterals és:
|
|
A vegades, pot haver-hi més d'un trajecte que passa a través d'un abantpassat comú, i a vegades pot haver-hi més d'un abantpassat comú. En tots els casos, el parentesc total és la suma del parentesc amb el que contribueix cada un dels trajectes.
L'abantpassat comú té, evidentment, una importància crítica en la determinació dels parentescs colaterals. Què passa quan aquest abantpassat és consanguini?. Hem vist que el coeficient de consanguinitat d'un individu és la probabilitat de que dos gens en un locus d'aquest individu siguin idèntics per descendència. Es dedueix que quan més alt sigui el coeficient de consanguinitat de l'abantpassat comú, major serà la probabilitat que transmeti el mateix gen a cada un dels dos parents colaterals que descendeixin d'ell, i, per tant major serà la probabilitat que els dos parents tinguin ambdos gens que són idèntics per descendència. De fet, si l'abantpassat comú és consanguini, el parentesc entre els dos parents colaterals que descendeixin d'ell, augmenta en una proporció igual al coeficient de consanguinitat de l'abantpassat comú. Això significa que el trajecte de l'abantpassat comú consanguini haurà de contenir un terme afegit en consideració a la seva endogàmia. Algebraicament, això equival a:
|
trajecte
|
+
|
(trajecte x FA)
|
=
|
trajecte (1+FA)
|
el què representa multiplicar (1/2) ^n+n' per cada trajecte de l'abantpassat comú consanguini per (1+FA), on FA és el coeficient de consanguinitat de l'abantpassat comú. Tenint present això, i utilitzant el símbol a pel parentesc, podem expressar el parentesc entre dos individus qualsevols com:
on el sumatori significa que s'ha d'efectuar la suma dels diferents trajectes (p), i en cas de que l'abantpassat fos consanguini, abans d'incloure el seu trajecte a la suma, s'ha de multiplicar per (1+FA)
La mateixa fórmula pot usar-se per calcular el parentesc directe simplement tenint present que en aquest cas només existeix una línia de descendència per a cada tracjecte, i per tant n'=0 per a cada trajecte.
Seguim amb l'exemple de la figura 2, amb l'encreuament entre B i C per produir un descendent O i considerem un gen escollit a l'atzar que B transmet a O.
Per calcular el coeficient de ocnsanguinitat d'O, necessitem calcular la probabilitat que l'altre gen del mateix locus en O (el gen procedent de C) sigui idèntic per descendència al gen rebut de B.
Per calcular aquesta probabilitat hem de recordar, en aquest cas, que el parentesc entre B i C és el número esperat de gens de C que són idèntics per descendència amb un gen escollit a l'atzar en el mateix locus de B.
Com que C és l'altre progenitor d'O i per tant existeix una probabilitat de 1/2 de que un gen qualsevol de C sigui transmès a O, es dedueix que la probabilitat que O rebi un gen de C que sigui idèntic per descendència amb el gen que O ha rebut de B, és igual al parentesc entre B i C, multiplicat per 1/2.
Això significa que: "El coeficient de consanguinitat d'un individu qualsevol és 1/2 del parentesc entre els pares d'aquest individu".
Tot això pot semblar complicat però amb uns exemples ho veurem més clar:
|
|
|
figura 4
|
És molt més fàcil si modifiquem l'arbre genaològic tradicional per convertir-lo en un diagrama de trajectes, en el que els individus implicats apareixen només una vegada i en el què les fletxes indiquen la direcció de l'herència (figura 5):
|
|
|
figura 5
|
Observem que al diagrama no apareixen tots els individus; s'han exclòs aquells que no són abantpassats comuns i que no es troben en cap trajecte entre l'abantpassat comú i l'individu en qüestió (en aquest cas D i E).
A continuació calcularem el parentesc entre els dos mig germans, B i C, i el coeficient de consanguinitat del seu descendet O. Començarem per construir la següent taula:
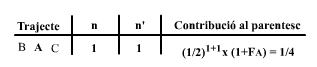 |
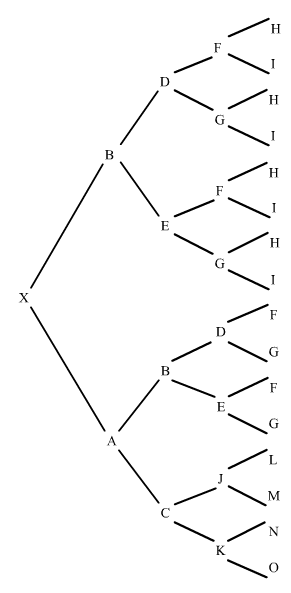
En aquesta taula, la A s'ha remarcat per indicar que es tracta de l'abantpassat comú en aquest trajecte. Com en el diagrama hi ha un sol trajecte, existeix una única entrada (fila) de dades a la taula que ens proporciona el parentesc entre B i C com:
 |
|
figura 6
|
Es dedueix per tant que el coeficient de consanguinitat d'O ve donat per:
|
figura 7
|
Fins aquí s'han exposat les definicions i les fórmules matemàtiques per entendre raonadament, i el més clar possibles, els conceptes tractats. No obstant, una vegada enteses aquestes nocions ja estem en disposició d'aplicar un mètode abreujat per arribar als mateixos resultats. Per això podem resumir en una, les fórmules de la figura 6 i 7:
|
figura 8
|
Essent el sumatori la suma de tots els trajectes possibles i n, el número de generacions que van de l'abantpassat comú des del costat patern al costat matern, i FA és el coeficient d'endogàmia de l'abantpassat comú A. A és un símbol general representatiu de qualsevol dels abantpassats susceptibles de contribuir a l'endogàmia de X. Si els abantpassats comuns no són endogàmics, aleshores FA = 0 i la fórmula s'escriu:
|
figura 9
|
Mirem ara un altre exemple en un pedegree una mica més complexe:
|
|
|
figura 10
|
L'individu X és el resultant de dos encreuaments consecutius respecte el pare B. En l'ascendència l'endogàmia es produeix en dos moments. El primer, l'aparellament de J amb B que dóna el trajecta XOJ; en el segon, l'aparellament d'O amb B que dóna el trajecte XO.
Ara procedim de la següent manera
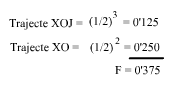 |
Què hem fet? Al primer trajecte hem comptat el número de generacions que van de B a X pel costat patern, i tornada a B pel costat matern fins a trobar el primer encreuament de B, donant-nos tres generacions, o sigui n=3, (l'abantpassat comú B mai no es comptavilitza).
En el segon trajecte hem actuat de la mateixa manera donant-nos dues generacions, o sigui n=2. Només ens ha faltat sumar aquestes endogàmies parcials.
Observem que tan D com E, tot hi estan als dos costats del pedegree (patern i matern) no es compten, donat que les seves contribucions a l'endogàmia estan incloses a la de B.
Observem, també, que aquest coeficient de consanguinitat F= 0'375 de l'individu X, és justament la meitat del parentesc que hi ha entre els seus pares (a=0'75), Figura 3.
Això corrobora el què hem dit quan explicàvem el càlcul del coeficient de consanguinitat: "El coeficient de consanguinitat d'un individu és sempre 1/2 del parentesc entre els seus pares".
Què passaria si al pedegree de la figura 10 es substituís la segona aparició de B per un germà M, i la tercera per un individu N sense cap parentesc respecte a B?. Això significaria que B no contribueix a l'endogàmia de X, en canvi D i E sí que ho fan. Vegem l'exemple:
|
|
|
figura 11
|
El trajecte per D és BXOM = (1/2)ˆ4 = 0'0625 i el d'E també és BXOM = (1/2)ˆ4 =0'0625. Intervenen dos abantpassats diferents i l'endogàmia total (Fx) és la suma dels dos trajectes buscats, és 0'125. Aquest exemple demostra que pot haver-hi més d'un abantpassat comú en un pedegree i que cada un d'ells farà la seva pròpia aportació al coeficient d'endogàmia (Fx).
Un cop vistos aquests exemples, podem resumir en tres regles bàsiques la determinació dels camins (trajectes) genaològics:
| 1era | L'abantpassat comú de l'individu X mai no es compta. |
| 2ona | Identificar sempre tots els camins (trajectes) possibles. |
| 3era | Els individus presents a ambdós costats del pedegree, mai no seran comptats més d'una vegada en el trajecte. |
Calculem ara el coeficient de consanguinitat d'un individu X, en el qual l'ascendent comú B és endogàmic (fill de germans, essent els seus avis també germans) i és a la vegada, pare i fill de l'individu X:
|
|
|
figura 12
|
El trajecte de B és XA o sigui (1/2)^2, però per ser B endogàmic hem de calcular el seu coeficient de consanguinitat a part:
 |
aplicant la fórmula:
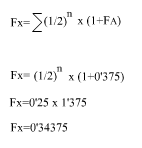 |
Aleshores, l'índex de consanguinitat de X és:
|
Fx= 0'34375 o el que és el mateix 34'375%.
|
Un altre exemple una mica més complicat. Substituim a l'individu C de l'exemple anterior per E que és la mateixa mare de B:
|
|
|
figura 13
|
Primer busquem tots els trajectes possibles:
 |
només falta calcular el trajecte de B, però, com que ja sabem que és endogàmic i el seu coeficient de consanguinitat observat en l'exemple anterior és 0'375:
trajecte de B, des de X fins a A:
|
|
Aleshores sumant els resultats de tots els trajectes ens dóna:
|
Fx= 0'5625 = 56'25%, un índex certament molt
alt.
|
La contribució a l'endogàmia dels abantpassats consignats en aquest exemple pot valorar-se de la manera següent: la major contribució pertany a l'individu B; en primer lloc perquè només es troba a una i dues generacions de distància de X, i en segon lloc per ser endogàmic ell mateix. La contribució d'E també és important, bàsicament per haver-se creuat amb el seu fill B. Si B és un gos excepcional, X podrà considerar-se un bon reproductor a causa de la contribució de B, j que aquest té un coeficient d'endogàmia força alt (37'50).
La pregunta sobre la conveniència de l'endogàmia no és fàcil de respondre. Malgrat això, hem de considerar que si un criador desitja fixar uns caràcters i obtenir gossos amb característiques pròpies i uniformitat en la descendència, és necessari cert grau d'endogàmia. La raó fonamental és que una raça pura o una casta homozigòtica no pot obtenir-se per altres medis. La selecció per sí sola no pot fer-ho. Pot fer-ho atípicament quan s'ha seleccionat un tipo de pares que presenta fenotips similars, en aquest caas, només alguns individus de la descendència tendiran, de tan en tan, a assemblar-se als pares.
L'endogàmia és necessària per "fixar els caràcters que amb tanta perceverància s'han estat seleccionant". Sens dubte l'endogàmia és bàsica per estabilitzar els resultats de la selecció.
Però, quan s'ha de començar l'endogàmia? Principalment els abenços més significatius de la selecció es realitzen durant els primers estadis. La disminució dels resultats acaba per tornar-se estacionària i és més difícil arribar a nous progressos. Aleshores, abans que es dilueixin els caràcters seleccionats, és quan hem de començar l'endogàmia per consolidar els resultats obtinguts. Aquesta és la filosofia simple i pura de la reproducció: la selecció ha de suspendre's i l'endogàmia iniciar-se quan el criador ho consideri oportú.
El terme "línia de sang" moltes vegades s'utilitzaa indiscriminadament i amb certa frivolitat per indicar un simple parentesc entre els gossos. Per alguns, n'hi ha prou amb què un semental s'aparelli aamb un determinat número de femelles i alguns dels seus descendents sobresurtin en les exposicions, per parlar de "línia de tal" o "línia de cual". Però evidentment hi ha alguna cosa més.
El terme no ha de ser usat a la lleugera sinó que s'ha de reservar per un criador amb trets únics que es repeteixin generació rere generació, fruit i colminació d'anys de cria selectiva ininterrompuda, acompanyada de certa quantitat d'endogàmia per assegurar la tendència hereditària.
Sabem que existeixen força gossos amb cert grau d'endogàmia. Però coeficients inferiors a 0'25 rarament seran perillosos. A partir d'aquesta xifra i per damunt de 0'5 denota una endogàmia de moderada a alta i el gos ha de ser vigilat.
Una de les objeccions formulada amb més freqüència contra l'endogàmia és que aquesta produeix anomalies. L'objecció és fonamental i mereix ser contestada. En principi s'ha de precisar que la possibilitat de que es dongui una anomalia és moltes vegades exagerada. En primer lloc, perquè l'endogàmia per sí mateixa no pot induir anomalies; encara que pot suscitaar l'aparició de qualsevol anomalia latent a la família.
L'aparellament aleatori o el creuament extern tendeixen a mantenir a ratlla els gens determinals recessius malgrat algunes aparicions insòlites o inesperades. És possible, inclús, que un gen deleteri sigui introduit a la cria, persisteixi durant algunes generacions i després aparegui a una generació sense que ningú entengui què és el què està passant.
Amb l'endogàmia la situació és diferent ja que tendeix a destapar els gens recessius indesitjables i per tant revela les anomalies latents. En aquest sentit pot considerar-se com una operació purificadora donat que a més de propiciar l'aparició de l'anomalia, contribueix, igualment, a la seva ràpida eliminació. Succeeix així, ja que els individus en els quals apareixen gens letals en homozigosis no tindran viavilitat. I en el cas que aflorin gens deleteris en homozigosis, s'evitarà la seva transmissió no fent procrear als individus portadors d'aquestes anomalies.
No obstant això, l'aparició aleatòria d'unes anomalies és infreqüent i imprevisible i no pot confondre's amb la depressió endogàmica.
La Depressió endogàmica és una possibilitat que s'ha de tenir present. Amb freqüència es diu que la endogàmia produeix un descens de la força vital dels reproductors; en efecte, la majoria de gens recesius deleteris es troben amagats en els heterozigots. Com que la consanguinitat disminueix la freqüència d'heterozigots, tendeix a desenmascarar aquests gens recessius danyats, en forma d'homozigots.
La pèrdua d'energia vital es deu a l'homozigoïtat creixent en els poligens indesitjables que controlen la salut, el vigor o la capacitat reproductora. L'efecte de cada un d'aquests es redueix, i passaria inadvertit, però l'efecte simultani de diversos d'ells, es tradueix en un animal d'aspecte malaltís sense motiu aparent, amb cert retard en el creixement , menys viu que els seus germans de cadellada i amb predisposició a totes les enfermetats que es presenten.
En les poblacions normals aquests poligens lleugerament deleteris es presenten com heterozigots i la seva presència passar desapercebuda fins que són posats en evidència per l'endogàmia.
Per explicar perque les línies endogàmiques tenen reduit el seu vigor i la fertilitat, pensem primer en la població en la qual els creuaments es produeixen, habitualment, entre individus no emparentats. Si en un individu apareix per mutació un al·lel deleteri recessiu, transmetrà aquest al·lel a la meitat dels seus descendents. Com que l'al·lel és recessiu, es pot estar transmaten i extenent durant generacions en aquesta mateixa població sense que es noti en el fenotip. Si es donés un creuament endogàmic entre dos membres de la població, portadors del recessiu, i tinguessin descendència entre ells, segons l'herència mendeliana, cada descendent tindria una probabilitat d'1/4 de ser homozigot recessiu, mostrant el fenotp aberrant.
Com que les mutacions deleteris acostumen a estar a freqüència baixa en les poblacions, dos individus qualsevols d'una població gran, encara que puguin portar mutacions deleteris en heterozigosis, tenen una probabilitat molt baixa de ser portadors del mateix al·lel recessiu. Per això la freqüència d'aparició d'anomalies genètiques en la descendència d'individus no emparentats és, proporcionalment, molt menor que en la d'individus emparentats.
En les línies endogàmiques en les que es força el creuament entre parents generació rere generació, aniran sortint homozigots recessius per molts al·les deleteris o letals, pel què cada vegada els individus seran més dèbils, menys fèrtils i les línies més difícils de mantenir. Les línies en les que apareguin letals en homozigosis es perdran, de manera que rere successives generacions d'endogàmia forçada les línies resultants no tindran letals, encara que poden tenir nombrosos al·lels deleteris per homozigisis.
Ens hem de preguntar per què els al·lels recessius que apareixen per mutació han de ser deleteris en homozigosis. La resposta és doble:
En primer lloc perque els al·lels mutants representen una variació enfront d'una situació prèviament adaptada.
| per exemple: si una impremta fa un error en imprimir una fulla d'un llibre i cambia a l'atzar una coma, una lletra o una paraula, és molt difícil que el text millori respecte el manuscrit original, quasi sempre empitjorarà. |
En segon lloc perque no té importància quants al·lels recessius "bons" existeixen; quan aparegui un homozigot per un al·lel "dolent", l'individu serà pitjor que si fos heterozigot en aquell locus. N'hi ha prou, per exemple, amb un sol al·lel mutant en homozigosis per a produir sordesa i mudesa, no té importància quants gens "bons" hi hagi per a altres caràcters.
Això no significa que tots els gossos siguin portadors d'aquests gens indesitjables, ni que l'endogàmia produeixi per defecte una descendència fràgil. L'endogàmia és inòqua en els animals inherentment sans i normals, però val la pena prendre precaucions.
Els poligens deleteris poden afectar qualsevol característica d'un gos normal, imperceptiblement al principi, més seriament després, si no s'han pres les disposicions convenients. Pot produir-se un descens del pes en néixer seguit de creixement insuficient, alteració de la capacitat reproductora en la forma de falta d'interès pel sexe contrari, falta de desig de copular o disminució de la freqüència copulatòria. En ambdós sexes la maduresa sexula es retarda. Els períodes de zel de la gossa són irregulars, el número de cadells per cadellada disminueix i les cadellades no arriben al pes normal. La depresió endogàmica sol presentar-se paulatinament, afectant a certs animals i a d'altres no. Per tant, convé canviar-la fent procrear exclusivament els gossos més sans i vigorosos. Si no s'aconsegueixen els resultats esperats només resta el recurs de creuaments externs. No obstant, s'ha d'estar molt alerta amb la integració de material genètic diferent, ja que pot comportar la introducció d'efectes inesperats.
|
SELECCIÓ
|
ENDOGÀMIA
|
| perpetuació d'alguns gens | fixació majoritària de gens |
| disminució reduida de l'heterozigositat | disminució ininterrumpuda de l'heterozigositat |
| augment de la similitud fenotípica | augment de la similitud genotípica |
A primera vista podria semblar que les conseqüències de la selecció i l'endogàmia són complementàries, i que n'hi ha prou amb què el criador seleccioni els animals apropiats i els faci criar entre sí per tal que els millors gens es fixin i s'obtinguin animals de primera qualitat.
En realitat resulta molt difícil concentrar tots els gens desitjables en uns pocs individuus per tal que puguin fixar-se en la descendència. L'endogàmia comporta l'esgotament de la variabilitat genètica i el gos deixa de progressar. Una possible solució de compromís consistirà en una endogàmia lleu o moderada. En canvi no pot existir compromís en matèria de selecció; aquesta ha de ser el més estricta possible, sdfasdfasdfa sdfasdfsaffd de la qualitat dels animals disponibles. Les fixacions dels gens han de prosseguir incansablement però sense presses, evitant que els trets indesitjables es fixen abans que el criador hagi arribat a eliminar-los. L'aparició de certs caràcters indesitjables són possibles en qualsevol moment del procés, d'aquí la necessitat de prosseguir la selecció.
Bibliografía:
Genética Veterinaria. F.W. Nicholas
Genética, Fundamentos y Perspectivas. M.J. Puertas
Genética para Criadores de Perros. Roy Robinson.
Del Cromosoma al Gen. Institut de Bioquímica Clínica.
|
JOAN FERRER i SIRVENT
LA BORDA D'URTX 17538 URTX (Girona) CATALUNYA Telf: +34-629-613399 e-mail: joanferrer@labordadurtx.org |